Projects
Using Machine Learning to Accelerate Global Optimization

|
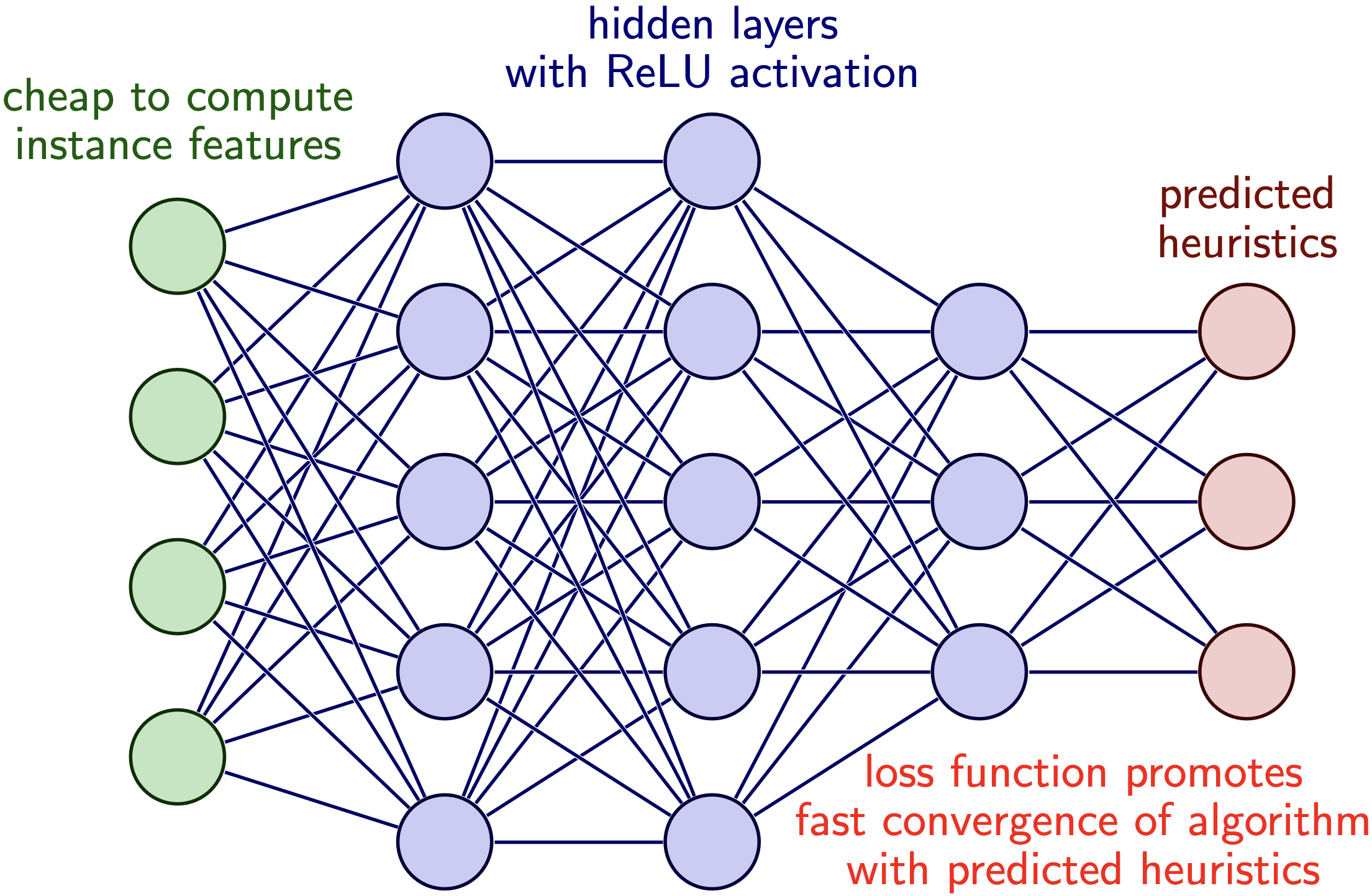
This project explores the use of ML to predict optimal instance-specific heuristic parameters within global optimization algorithms without sacrificing global optimality guarantees. We have devised algorithms to optimally partition variable domains for piecewise convex relaxation of nonconvex problems. Our ML algorithms are able to accelerate the solution of challenging problems by up to three orders of magnitude for specific instances and families of nonconvex problems by an order of magnitude on average! |
|


This project explores the use of ML to predict optimal instance-specific heuristic parameters within global optimization algorithms without sacrificing global optimality guarantees. We have devised algorithms to optimally partition variable domains for piecewise convex relaxation of nonconvex problems. Our ML algorithms are able to accelerate the solution of challenging problems by up to three orders of magnitude for specific instances and families of nonconvex problems by an order of magnitude on average!
Enhancing the Resilience of the Power Grid to Extreme Weather Events
|
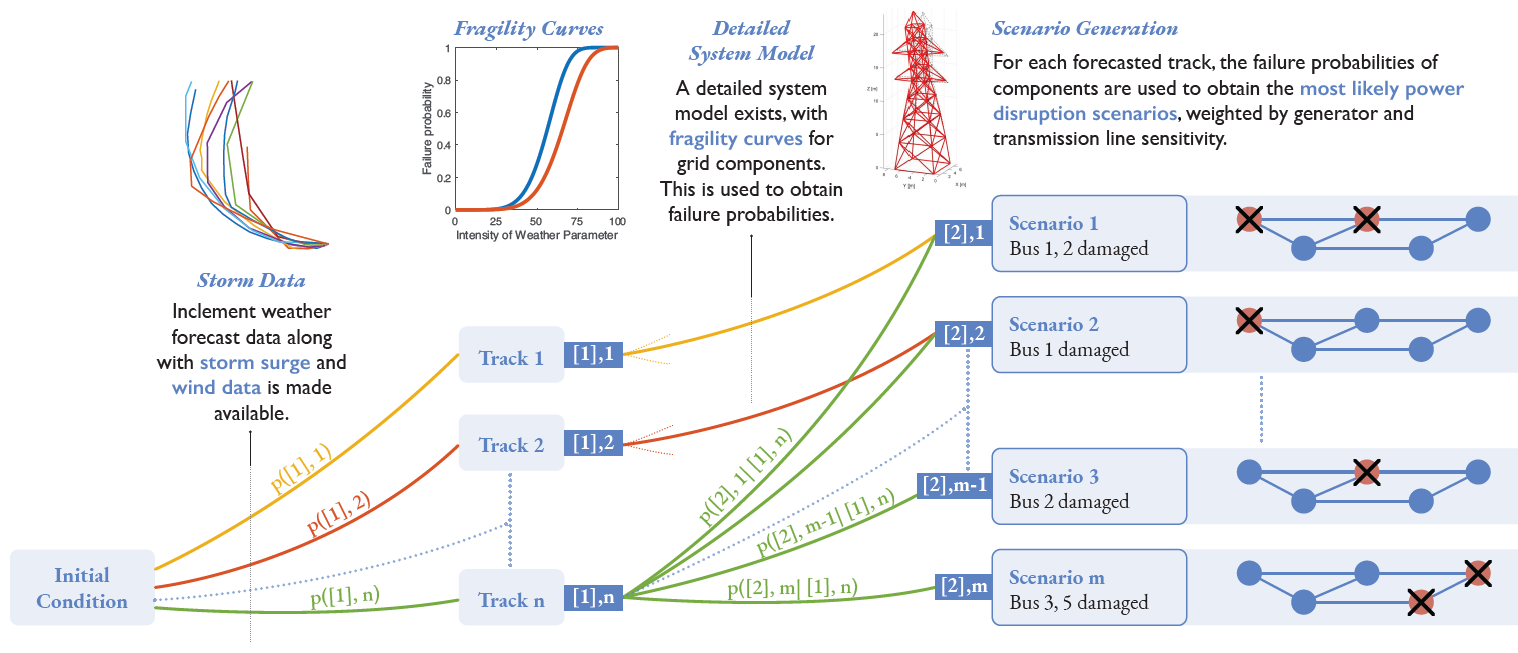
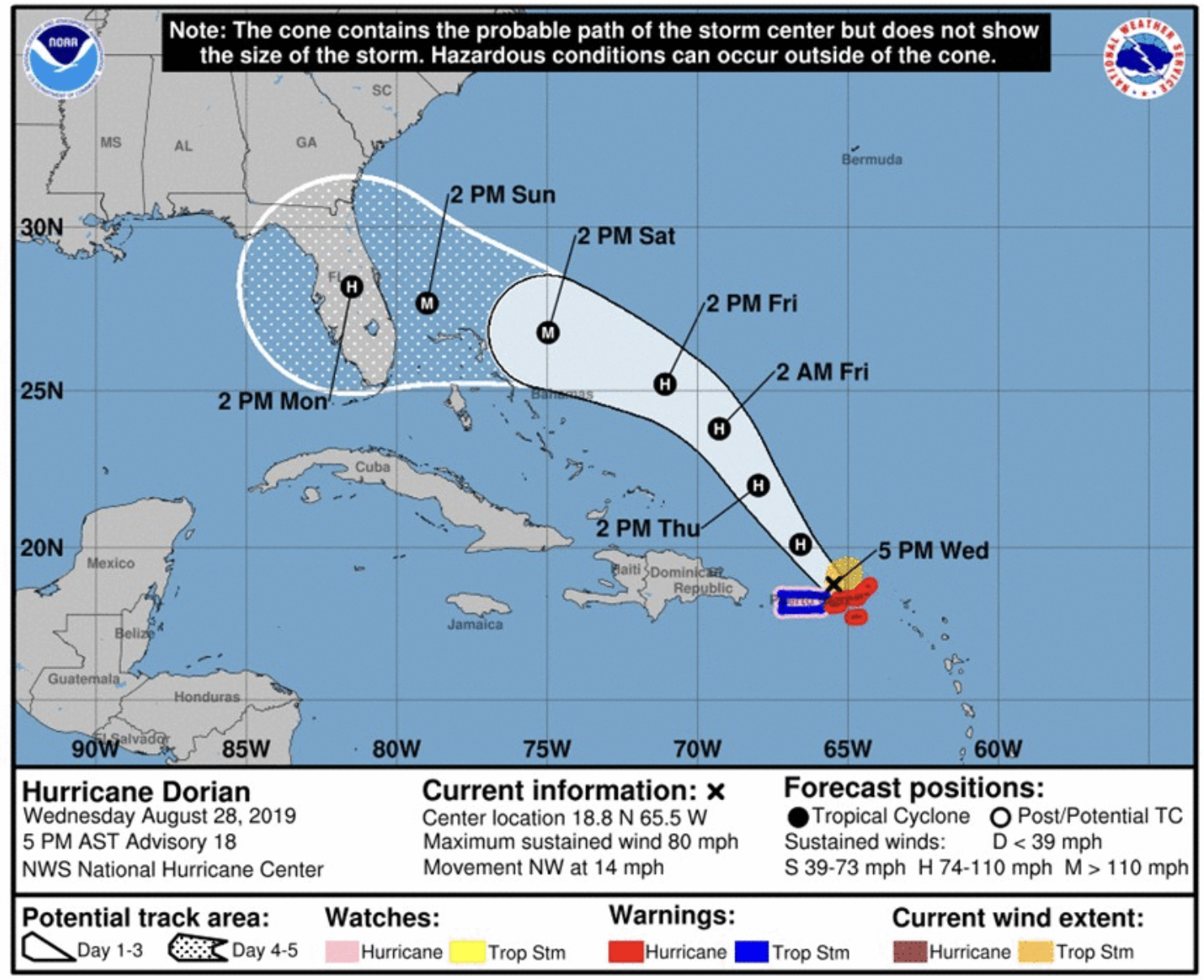
This project aims to leverage ensemble forecasts of extreme weather events (such as hurricanes and winter storms) to make proactive grid operation decisions and mitigate power outages. We model the operational resilience of the grid using multistage stochastic programming and use stochastic dual dynamic programming to joinly optimize anticipative and restorative actions. Our preliminary results show that using hurricane forecasts to make proactive decisions can reduce load shed by up to 5% on average! |


This project aims to leverage ensemble forecasts of extreme weather events (such as hurricanes and winter storms) to make proactive grid operation decisions and mitigate power outages. We model the operational resilience of the grid using multistage stochastic programming and use stochastic dual dynamic programming to joinly optimize anticipative and restorative actions. Our preliminary results show that using hurricane forecasts to make proactive decisions can reduce load shed by up to 5% on average!
Integrating Machine Learning Predictions Within Stochastic Optimization
|
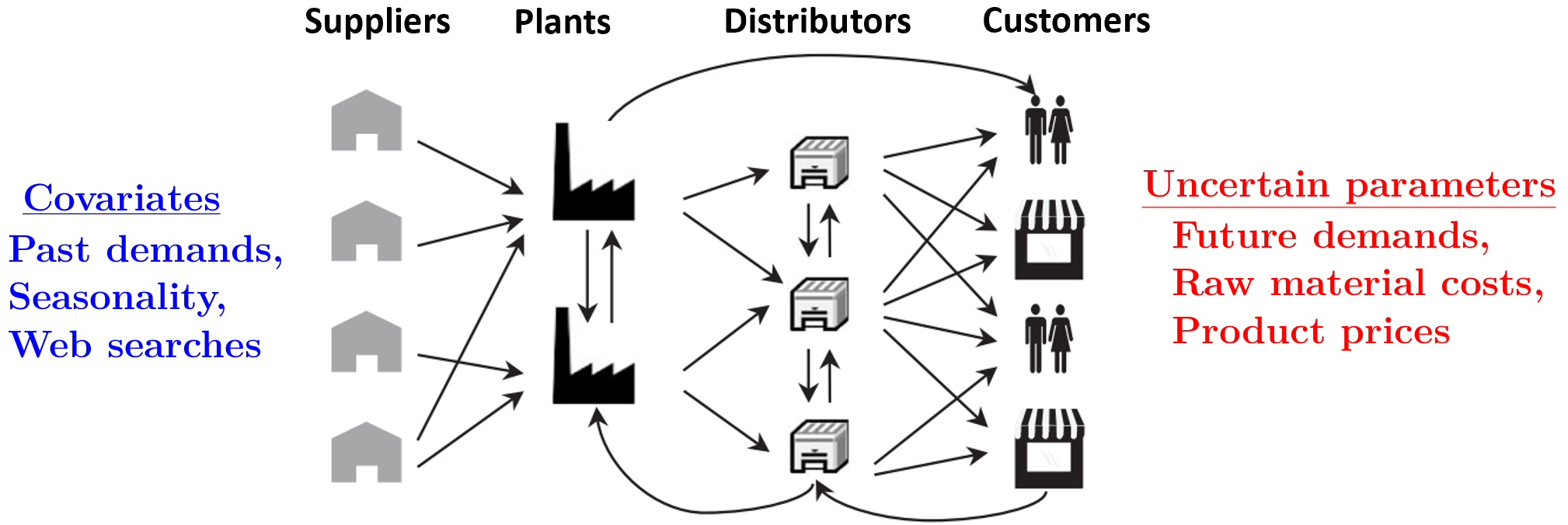
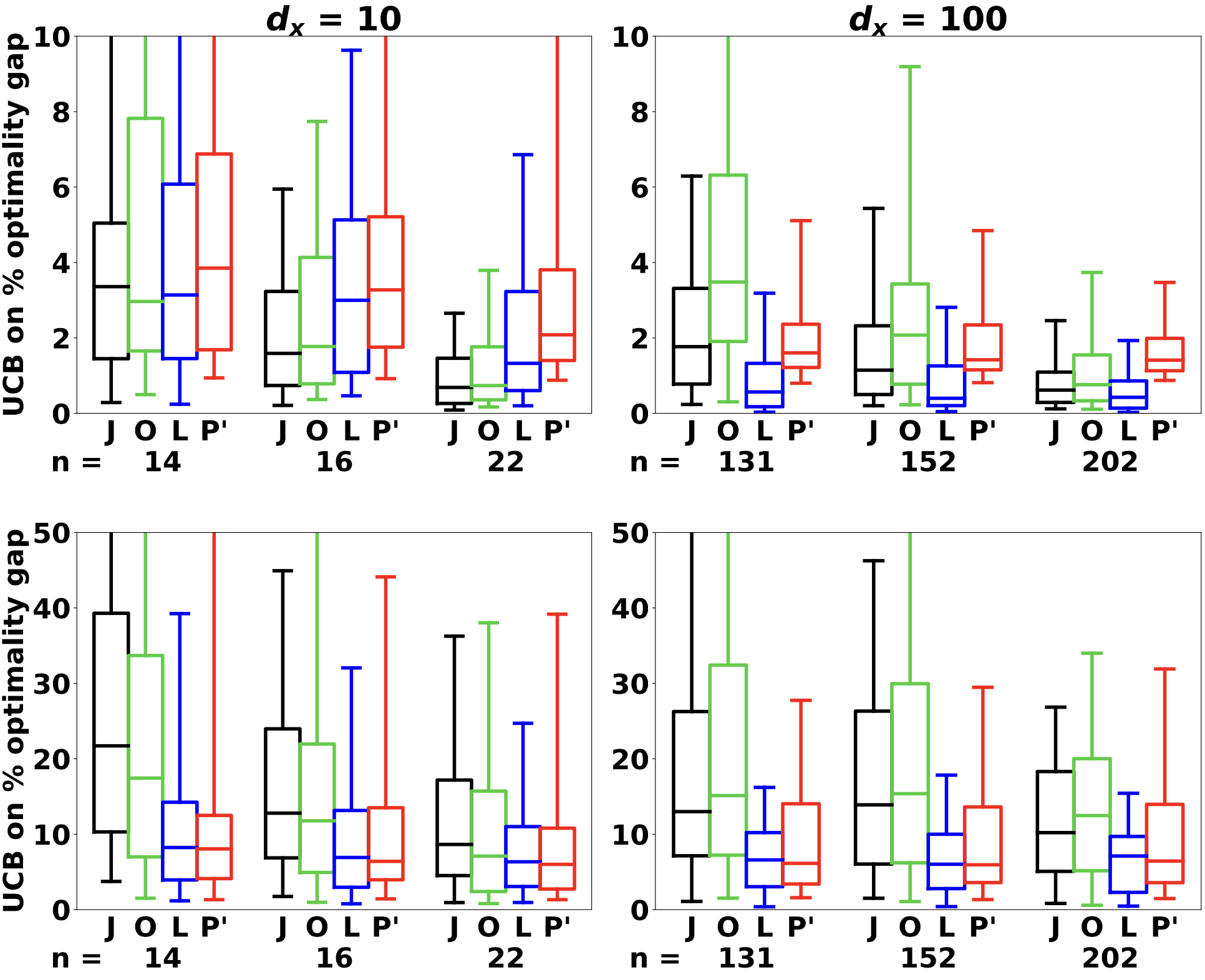
Uncertain parameters in optimization models can often be predicted using covariate information. For instance, product demands can be estimated using seasonality, historical data, and web search results for use in a supply chain model. We investigate a flexible framework for data-driven decision-making under uncertainty that integrates an ML prediction model and its residuals within a sample average approximation, and identify conditions for convergence as the sample size increases. Our numerical experiments demonstrate the advantages of our data-driven formulations in the limited data regime. |
|


Uncertain parameters in optimization models can often be predicted using covariate information. For instance, product demands can be estimated using seasonality, historical data, and web search results for use in a supply chain model. We investigate a flexible framework for data-driven decision-making under uncertainty that integrates an ML prediction model and its residuals within a sample average approximation, and identify conditions for convergence as the sample size increases. Our numerical experiments demonstrate the advantages of our data-driven formulations in the limited data regime.
Algorithms for Nonconvex Stochastic Programming
|
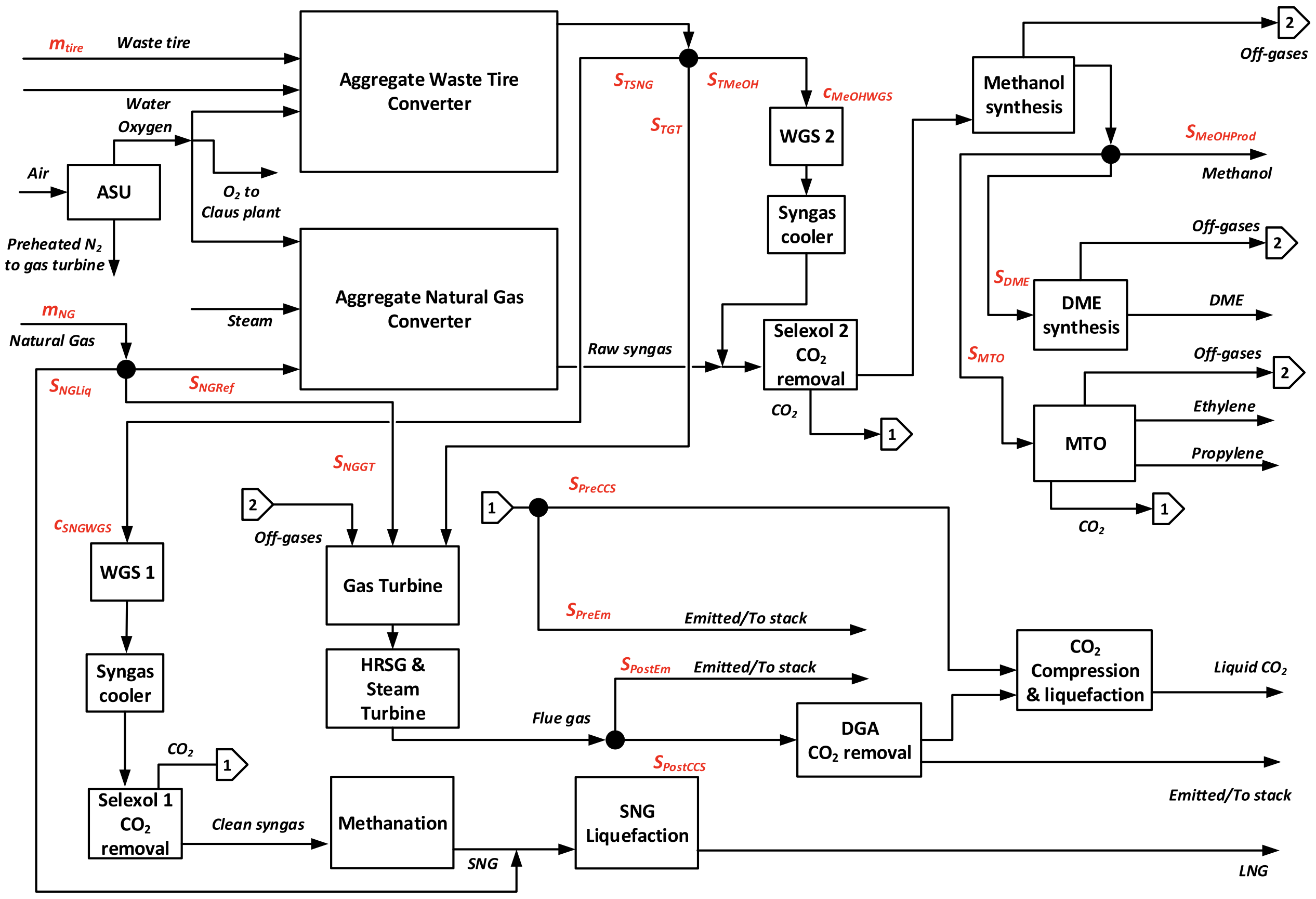
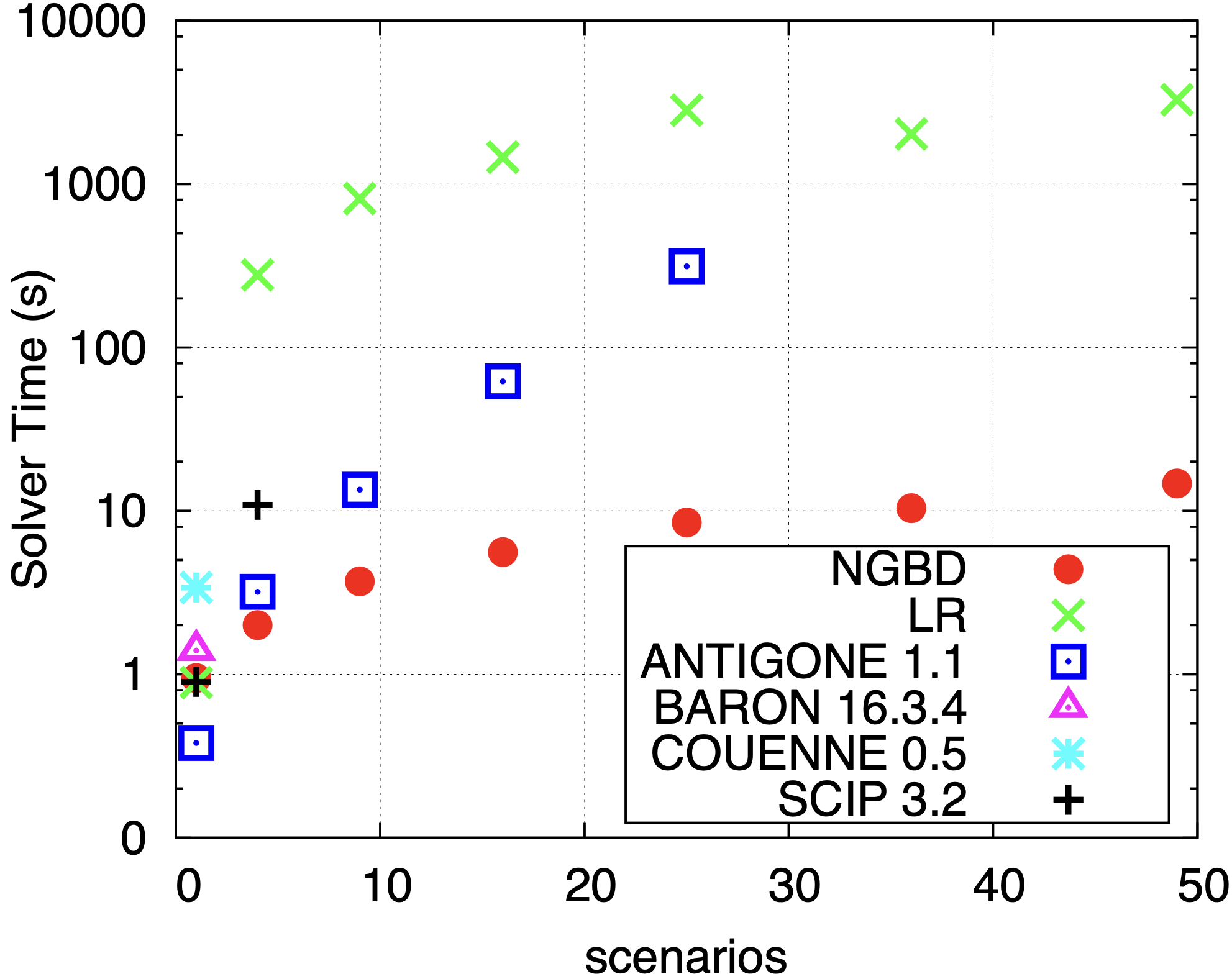
Two-stage stochastic mixed-integer nonlinear programs (MINLPs) are widely used for optimization under uncertainty in areas like energy, finance, and supply chain management. These models are difficult to solve due to nonconvex constraints and discrete decision variables. We design a decomposition algorithm and a software for two-stage stochastic MINLPs. In collaboration with NTNU, we have used it to design a hybrid waste tire and natural gas polygeneration system, achieving a 100% increase in expected net present value over a nominal design. |


Two-stage stochastic mixed-integer nonlinear programs (MINLPs) are widely used for optimization under uncertainty in areas like energy, finance, and supply chain management. These models are difficult to solve due to nonconvex constraints and discrete decision variables. We design a decomposition algorithm and a software for two-stage stochastic MINLPs. In collaboration with NTNU, we have used it to design a hybrid waste tire and natural gas polygeneration system, achieving a 100% increase in expected net present value over a nominal design.
Convergence Rate of Branch-and-Bound Algorithms
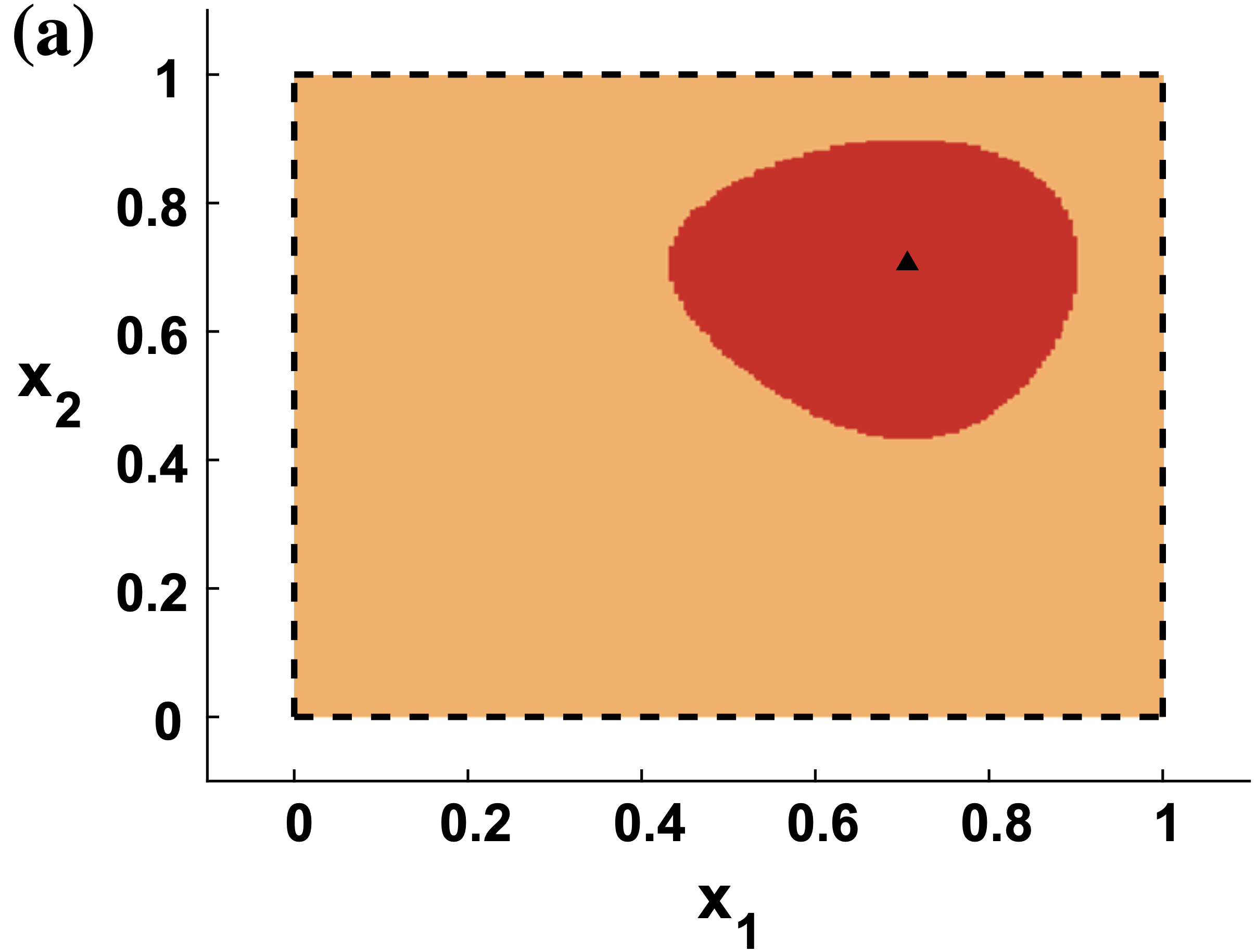
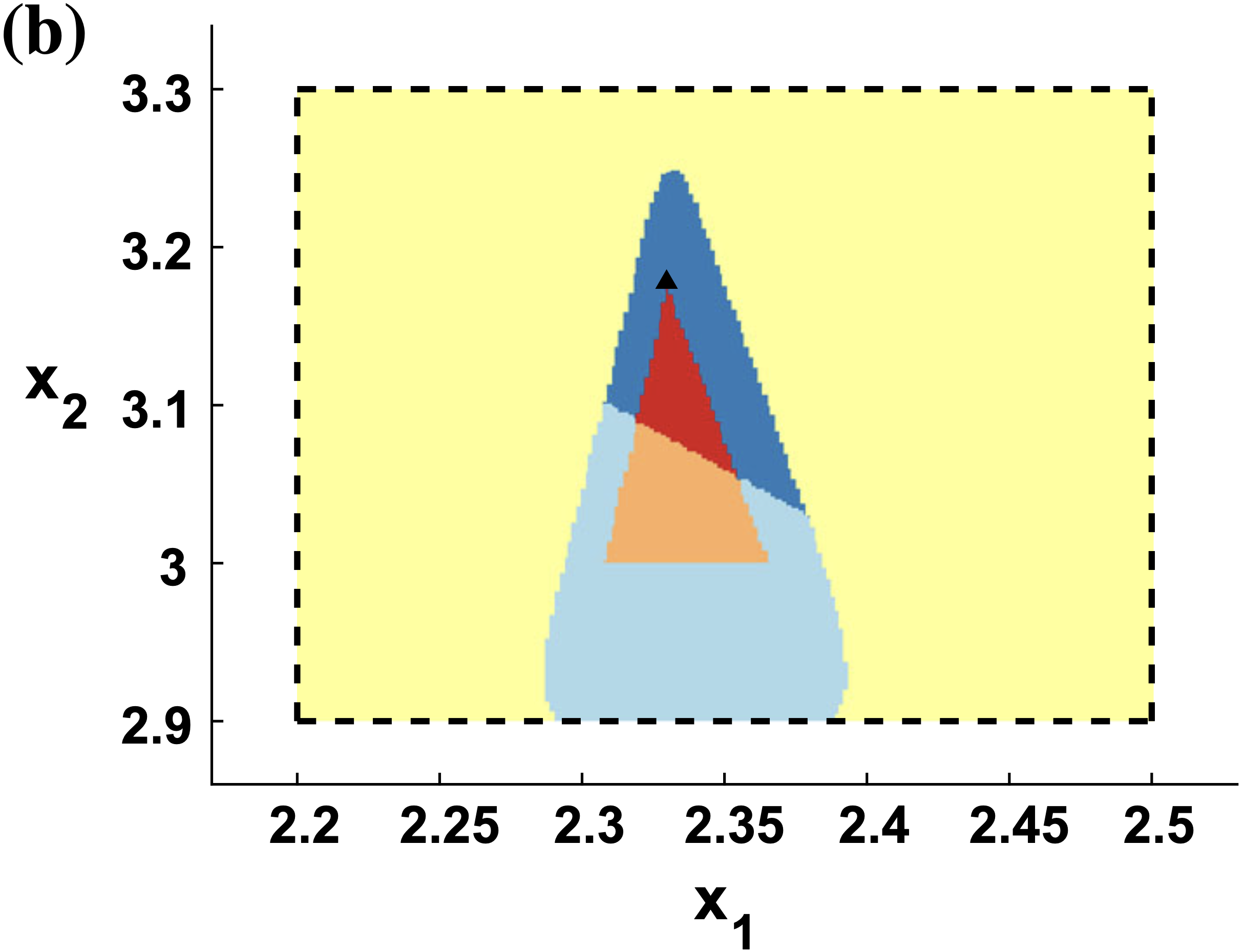
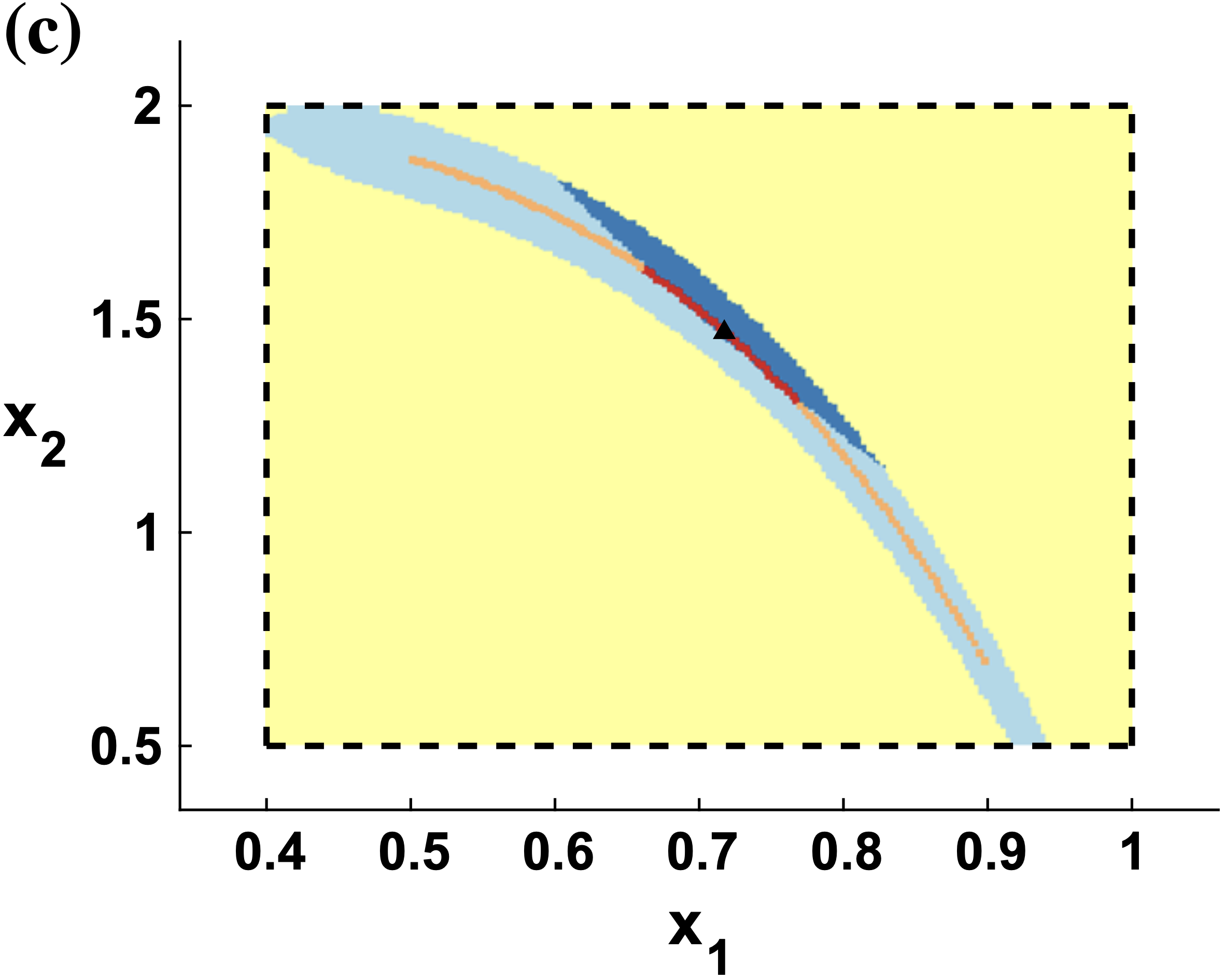
Analysis of the cluster problem in global optimization for (a) an unconstrained problem, (b) an inequality-constrained problem, and (c) an equality-constrained problem.
|
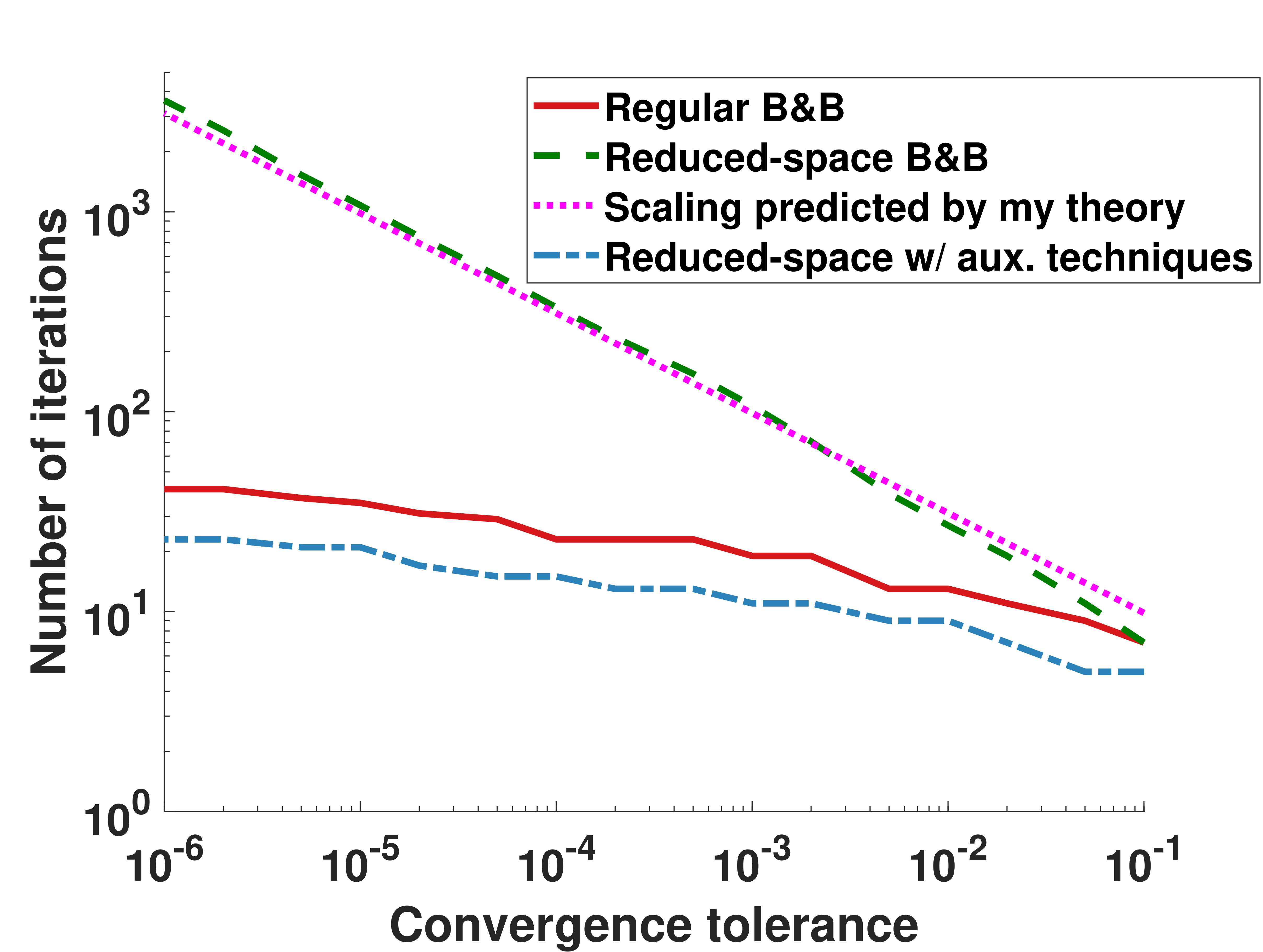
Branch-and-bound (B&B) algorithms are the primary framework for solving nonconvex problems to global optimality. However, a major drawback is that they can require an exponential number of iterations relative to the search space dimension to converge. Reduced-space B&B algorithms attempt to address this by branching on a lower-dimensional subspace, but their convergence rate remains poorly understood. We analyze the convergence rate of B&B algorithms and find that reduced-space methods may be impractical without the use of auxiliary domain reduction techniques to speed up convergence. |
|




Branch-and-bound (B&B) algorithms are the primary framework for solving nonconvex problems to global optimality. However, a major drawback is that they can require an exponential number of iterations relative to the search space dimension to converge. Reduced-space B&B algorithms attempt to address this by branching on a lower-dimensional subspace, but their convergence rate remains poorly understood. We analyze the convergence rate of B&B algorithms and find that reduced-space methods may be impractical without the use of auxiliary domain reduction techniques to speed up convergence.